The Independent Sentinel #36
Modelos fundacionales, problemas modernos y la infinita complejidad de la realidad
¡Hola!
Soy Javier Fuentes, de Akoios. Te doy la bienvenida a esta nueva edición de The Independent Sentinel, la newsletter en la que hablamos sobre Inteligencia Artificial y Ciencia de Datos a través de avances, casos de uso e historias.
Suscríbete si aún no lo has hecho para recibir cada edición directamente en tu email.
En esta edición hablaremos de unos modelos ajustables, de polémicas del siglo XXI y de dibujos infinitos.
¡Vamos allá!
🎼 Quieres banda sonora? ¡Dale al Play!
1. Tendencias 📊
🧱 Modelos fundacionales
Como estamos viendo durante los últimos meses, el desarrollo de nuevos modelos está avanzando a un ritmo vertiginoso.
En buena medida, esto viene dado por una característica de ciertos modelos que los hace especialmente versátiles. Veamos en qué consiste esto.
Históricamente, cada modelo requería un entrenamiento ad-hoc, usualmente lento y costoso en términos computacionales. Para cada nueva aplicación, un nuevo modelo debía ser diseñado y entrenado de manera específica.
Esta nueva ola de modelos que estamos viendo está reemplazando estos modelos clásicos “especialistas” por otros modelos que podemos llamar “fundacionales”. Esto es, modelos entrenados con gigantescos conjuntos de datos que pueden ser posteriormente ajustados para una tarea o labor específica. Ejemplos de estos modelos fundacionales serían algunos tan conocidos como GPT-3, BERT o Dall-E 2.
La parte más interesante es que, usando técnicas de aprendizaje auto-supervisado o transfer learning, es posible incorporar información específica de un dominio de manera relativamente sencilla sin tener que volver a re-entrenar desde cero el modelo.
Un ejemplo fantástico es el uso de un modelo generativo de imágenes como Stable Diffusion junto con DreamBooth, una herramienta con la que podemos incluir las imágenes que deseemos para ajustar el modelo. En el siguiente vídeo puedes ver una guía de uso:
Obviamente, no todo son buenas noticias en este tipo de modelos ya que, al usar arquitecturas tan sumamente complejas como base, se complica la explicabilidad de los mismos.
Tal está siendo el interés sobre este tipo de modelos que se están creando distintos grupos de investigación en este ámbito como, por ejemplo, este de la Universidad de Stanford.
Todo parecer indicar que estos modelos fundacionales serán los ladrillos con los que se construirán las aplicaciones de IA de aquí en adelante.
💫 Un modelo efímero
48 horas.
48 horas ha sido el tiempo que ha tardado Meta en retirar el acceso público a Galactica, el último modelo que ha liberado la empresa de Mark Zuckerberg.
Galactica es un modelo creado con la ambiciosa intención de “organizar la ciencia”. Según los autores, se puede entender este modelo como la evolución de un motor de búsqueda especifico para la literatura científica con increíbles capacidades adicionales.
Imagina que quisieras entender los últimos avances en, por ejemplo, biología evolutiva. El enfoque clásico consistiría en pasar horas y horas leyendo cientos de papers y consultando diversas fuentes para conseguir formarse una mínima idea sobre el tema.
La solución propuesta por Galactica para esta situación sería simplemete realizar una pregunta (prompt) sobre la temática (por ejemplo, “Últimos avances en biología evolutiva”) para que el modelo generase un artículo tipo Wikipedia (incluyendo fuentes) para dar respuesta a nuestra pregunta.
Sencillamente increíble. No solo eso sino que, como se explica en el repositorio del modelo, Galáctica es capaz de realizar:
📚 Predicción de citas
🔢 Predicción de notación LaTeX
🤔 Razonamiento
⚛️ Generación de moléculas
🧑🔬 Anotación de proteínas
❓Respuesta de preguntas
Hace apenas dos semanas, el pasado 15 de Noviembre, se publicó de manera pública el modelo y el paper que lo acompañaba.
Según se explica en la publicación, el modelo fue entrenado con un enorme corpus compuesto por una cantidad ingente de publicaciones científicas: 48 millones de papers, libros de texto, notas y sitios web como la Wikipedia.

Para evitar malentendidos y manejar las expectativas ante una herramienta de estas características en su versión inicial, en la propia web constaba un mensaje grande, claro y conciso alertando sobre el uso de un modelo así:
"NEVER FOLLOW ADVICE FROM A LANGUAGE MODEL WITHOUT VERIFICATION."
Pese a todo, tan pronto como se liberó el modelo, comenzaron las pruebas por parte de los usuarios y, tras ello, llegó una inesperada avalancha de críticas al modelo por considerarlo “peligroso”, “no ético” o “distorsionador”, principalmente por su incapacidad de diferenciar lo cierto de lo que no lo es en el ámbito científico.
Tal fue el impacto de las críticas que Meta decidió a las 48 retirar el acceso público:

Mi opinión a este respecto es bastante clara. En ningún momento Meta indicó que las respuestas de este modelo fuesen a ser reales, fiables o precisas, por lo que nadie debería verse sorprendido por los resultados.
En este sentido, creo que es mejor que se libere un modelo aunque funcione mal. Este es el primer paso para que toda la comunidad pueda trabajar para probarlo y mejorarlo. Si hubiese que esperar a que un modelo fuese perfecto para liberarlo, nunca lo haríamos.
2. Historias 📔
☁ Las nubes no son esferas
“Why is geometry often described as “cold” and “dry?” One reason lies in its inability to describe the shape of a cloud, a mountain, a coastline, or a tree. Clouds are not spheres, mountains are not cones, coastlines are not circles, and bark is not smooth, nor does lightning travel in a straight line.”
Benoit Mandelbrot.
Con este bello párrafo es cómo comenzaba Benoit Mandelbrot su principal obra: “La geometría fractal de la naturaleza”.
Mandelbrot venía a decirnos que la perfección, frialdad y pureza de la geometría Euclidiana es lo que nos aleja de ella, porque no se corresponde con nuestra realidad: áspera, compleja y -aparentemente- caótica.
¿Qué tipo de geometría podría representar la realidad?
🧮 Una clara vocación
Benoit Mandelbrot nació el Varsovia en el seno de una familia judía durante la Segunda República polaca. Durante su niñez tuvo la suerte de estar en contacto estrecho con uno de sus tíos, Szolen Mandelbrojt, un matemático que residía en París.
Justamente a París, es donde sus padres decidieron emigrar en 1936 y donde estuvieron hasta el comienzo de la Segunda Guerra Mundial, momento en el que, por la invasión nazi, se mudaron al pequeño pueblo de Tulle.
Mandelbrot mostró una vocación manifiesta por las matemáticas desde la niñez, disciplina en la que pudo profundizar tanto en la École Polytechnique (1945–47) de París como en Estados Unidos donde tuvo la oportunidad de estudiar en el California Institute of Technology (1947–49) y bajo la tutela del mismísimo John Von Neumman en Princeton.
💻 Un gran fichaje
En 1958, Mandelbrot se mudó definitivamente a Estados Unidos al ser contratado por IBM, lugar en el que trabajó durante 32 años.
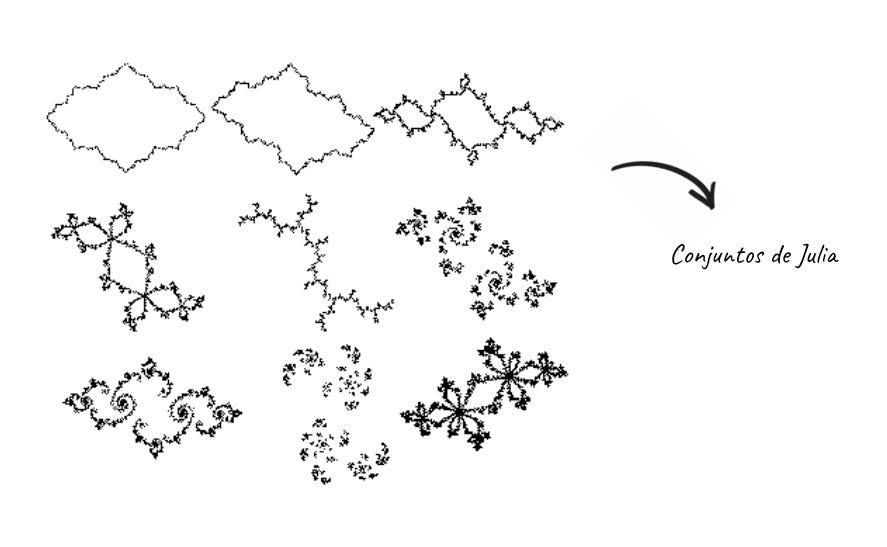
El fichaje de Mandelbrot por parte de IBM fue una afortunada casualidad. Mientras Mandelbrot trabaja en la identificación de problemas en líneas de transmisión de datos usando los medios de computación que tenía disponibles en IBM, tuvo la libertad de usar estos mismos ordenadores para trabajar en un problema que le había explicado su tío hacía tiempo y que estaba basado en el trabajo de un matemático francés llamado Gaston Julia.
Gaston Julia había creado una serie de conjuntos obtenidos a partir de la iteración de números complejos mediante una función. La representación gráfica de estos conjuntos era figuras como las siguientes:
Mandelbrot usó las potentes computadoras de IBM para trabajar sobre este tipo de ecuaciones, manipulando los números millones y millones de veces y representando los resultados.
El resultado que obtuvo era una extraña forma parecida a un insecto pero, al acercarse más, quedó perplejo al comprobar que los extremos de esa figura, parecían repetir a menor escala la estructura principal
Mandelbrot acababa de descubrir la geometría fractal.
∞ Los fractales
Un fractal es un patrón infinito e infinitamente complejo que se parece a sí mismo en diferentes escalas. Como hemos visto, estos patrones se crean iterando funciones matemáticas recursivas que se llaman a sí mismas en un bucle infinito.
Según Mandelbrot, estos patrones cumplían estas características:
Son demasiado irregulares para ser descrito en términos geométricos tradicionales (segmentos, circunferencias, …)
Poseen detalle a cualquier escala de observación.
Son autosimilares (exacta o aproximadamente).
Si lo piensas, los patrones fractales nos son extremadamente familiares ya que se repiten de forma sistemática en la naturaleza: ramas de árboles, sistemas circulatorios, copos de nieve, plantas, ríos, nubes, cristales, etc.

Además, hay otro aspecto terriblemente interesante y es que, en sistemas totalmente complejos y de tamaños extremadamente distintos, podemos ver como ciertos patrones se repiten como si de un fractal se tratara:

La imagen que Mandelbrot generó y de la que hablamos antes, no era otra que la representación del conocidísimo “Conjunto de Mandelbrot” o “Conjunto M”. Tal vez no te suene el nombre, pero seguro que si su representación gráfica:
Nada mejor que un ejemplo interactivo para poder navegar por el fractal y experimentar la infinitud de estos objetos geométricos.
∞ Usos inesperados
Lejos de ser simplemente una herramienta curiosa o llamativa, los fractales tienen usos en muy diversos campos, desde la biología y la medicina hasta las telecomunicaciones.
Puede sorprender que un campo específico en el que Mandelbrot utilizó los fractales fuese el de las Finanzas. En su obra “The (Mis)Behavior of Markets”, Benoit detallaba un método para modelar activos financieros como acciones, bonos o commodities.
Mandelbrot ya estaba intuyendo la idea que le haría mundialmente conocido antes incluso de acuñar el término “fractal”. En una de sus primeras publicaciones (“On the variation of certain speculative prices (1963)”, Benoit explicaba como, si eliminamos las escalas de precio y tiempo, los registros anuales, mensuales y diarios tendían a parecerse tremendamente 🤯.
🤖 Los fractales y la Inteligencia Artificial
Como ya estarías suponiendo, esta historia no podría acabar sin vincular el extraordinario trabajo de Mandelbrot con la Inteligencia Artificial. Veamos cuál es esta relación.
Los sistemas de reconocimiento de imágenes que hemos venido utilizando hasta el momento deben ser entrenados con una cantidad inmensa de imágenes reales, una labor ardua y costosa, pese a que bases de datos como ImageNet han facilitado increíblemente esta labor.
La pregunta es: ¿qué pasaría si pudiésemos crear imágenes de entrenamiento de manera automática e ilimitada?
Un equipo de investigadores de Japón ha desarrollado un modelo de entrenamiento que, en vez de usar imágenes reales, es capaz de generar imágenes sintéticas de manera infinita usando fractales.
Como explican en su paper, han sido capaces de crear FractalDB, una base de datos que incluye infidad de imagenes generadas con fractales: hojas, copos de nieve, caparazones de caracoles, etc.
A tenor de los resultados, parece que el entrenamiento de modelos con este tipo de imágenes es casi igual de eficaz que el realizado con imágenes reales y, aparentemente, será posible generar datasets sintéticos para usos como este.
Es imposible no pensar donde estará el límite de la IA si imaginamos modelos fundacionales (como los que hemos visto al comienzo) que se puedan auto-entrenar con datasets auto-generados con fractales. Todo parece ciencia-ficción hasta que deja de serlo.
Sin saberlo, Mandelbrot acabó creando una nueva disciplina matemática que él mismo llegó a utilizar para las finanzas, la hidrología, la física, el lenguaje y para el desarrollo de las propias matemáticas.
Al ser preguntado en una de sus últimas entrevistas sobre cómo se veía a sí mismo, Mandelbrot, lejos de contestar que como un matemático, respondió que se consideraba un simple narrador de historias.
No se me ocurre una mejor descripción para el descubridor de los fractales, unos patrones que, mirados con atención, no hacen más que contarnos historias sobre los fenómenos de nuestro universo.
¡Gracias como siempre por leer hasta aquí!
¿Te gusta The Independent Sentinel? ¡Comparte esta publicación para ayudarnos a llegar a más gente!
Si tienes comentarios o quieres iniciar una conversación, recuerda que puedes hacerlo aquí.
Si te has perdido alguna edición de la newsletter o quieres volver a leerlas, puedes acceder a todas aquí.
👉 ¿Quieres conocer nuestra tecnología Titan? No te pierdas nuestra serie de tutoriales publicados en Medium.
👉 Si te interesa, puedes solicitar un acceso gratuito para probar Titan aquí https://lnkd.in/gPz-2mJ