The Independent Sentinel #13
La maldición de la dimensionalidad, un repositorio increíble y el hombre más inteligente que ha pisado la tierra
¡Hola!
Soy Javier Fuentes, de Akoios, bienvenido de nuevo a The Independent Sentinel, la newsletter mensual para todos los públicos en la que hablamos de Ciencia de Datos e Inteligencia Artificial.
Si aún no te has suscrito, hazlo ahora y recibe cada publicación en tu email:
En esta edición hablaremos de la maldición de la dimensionalidad, de un GitHub para Machine Learning y del padre de la computación moderna: John Von Neumann.

¡Allá vamos!
🎼 ¿Quieres banda sonora? ¡Dale al Play!
1. Ciencia de Datos
La Maldición de la Dimensionalidad
En Ciencia de Datos, es muy común trabajar con datos de alta dimensión. Por ejemplo, si estamos desarrollando un modelo inmobiliario en el que manejamos 10 parámetros (precio, m2, nº habitaciones, nº baños, distancia al centro, barrio, piscina, terraza, garaje y año de construcción), estaremos trabajando en un espacio de 10 dimensiones.
Otro ejemplo sería el de tratamiento de imágenes. Si manejamos imágenes de 100x100 píxeles, estaremos trabajando en un espacio de 10000 dimensiones (cada pixel representaría una dimensión).
La idea de La Maldición de la Dimensionalidad -concepto acuñado por Richard E. Bellman- viene a decir que, según añadimos dimensiones, se va incrementando el coste computacional y se va haciendo exponencialmente más complicado hacer predicciones precisas en modelos de regresión o clasificación.
La idea clave es que, según crece el número de dimensiones, la cantidad de datos necesaria para poder hacer generalizaciones crece exponencialmente.
Imaginemos que tenemos 5 muestras en un conjunto de datos de entrenamiento. Si estuviésemos trabajando con una dimensión (imagen de la izquierda), podríamos representar con cada una de las cajas (muestras) una parte de esta dimensión.
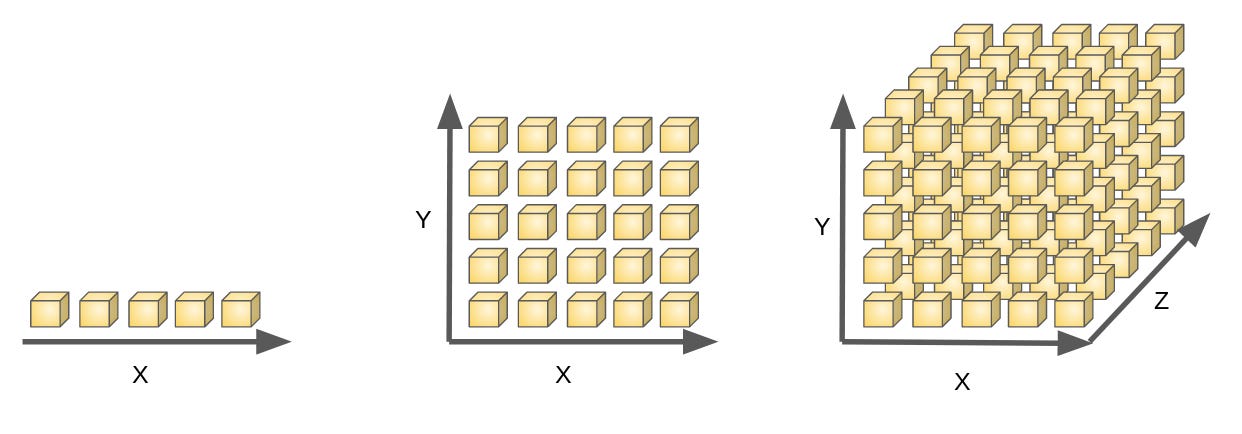
Una explicación gráfica de la Maldición de la dimensionalidad
Si empezamos a trabajar con dos dimensiones (imagen central), necesitamos 5² = 25 cajas para “muestrear” todo el espacio y, por último, si trabajamos con 3 dimensiones, necesitaríamos 5³ = 125. Como se observa, el crecimiento es exponencial y responde, en este caso, a la expresión 5^n.
Este crecimiento en la complejidad es una idea es clave cuando trabajamos con modelos de Machine Learning ya que, no siempre añadir nuevas dimensiones a un modelo tiene efectos positivos en la predicción.
De hecho, el efecto de añadir dimensiones a un modelo sigue el siguiente patrón llamado Fenómeno de Hughes:
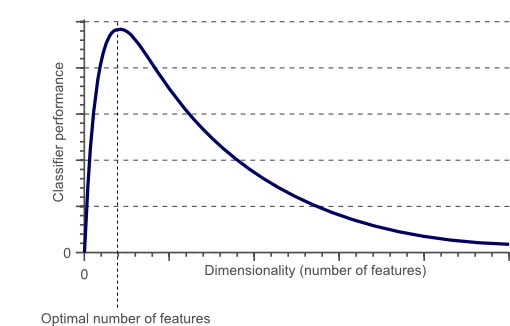
El fenómeno de Hughes
Cómo se ve en la gráfica, el rendimiento del modelo aumenta según se añaden dimensiones hasta un punto óptimo a partir de cuál, el añadir nuevas dimensiones afecta negativamente en el capacidad predictiva del modelo.
Las implicaciones de este fenómeno (la complejidad creciente en los sistemas) van más allá del Machine Learning y se encuentran en todos los órdenes de la naturaleza.
Como explica Taleb en este artículo, el gusano C elegans, el primer ser vivo del que se secuenció su ADN, tiene alrededor de 300 neuronas y, simplemente el hecho de añadir una más (hasta las 301), podría duplicar la complejidad de su cerebro.
Nuestro amigo el gusano C Elegans
Teniendo en cuenta que en altas dimensiones, por ejemplo pasar de 1000 a 1001, puede hacer que la complejidad se multiplique por un billón, es inmediato intuir la inabarcable complejidad emergente de un cerebro humano compuesto por aproximadamente 100 mil millones de neuronas.
La tesis de Taleb es que en sistemas complejos, los resultados no sólo dependen de la naturaleza de los componentes si no, sobre todo, de las interacciones entre ellos. Y, como hemos visto, estas interacciones pueden ser infinitamente complejas debido a la Maldición de la Dimensionalidad.
Understanding how the subparts of the brain (say, neurons) work will never allow us to understand how the brain works.
Veremos si algún día somos capaces de manejar esta complejidad y empezar a entender la inmensa complejidad de un sistema como el cerebro humano.
Modelos y Algoritmos 💻
Hace poco descubrí una página que ha ido directa a mis favoritas en lo relativo a Ciencia de Datos. Papers With Code es una suerte de GitHub para científicos de datos dónde se pueden encontrar no solo todo tipo de papers sino también el código asociado a los mismos.
Además, todo está perfectamente clasificado para poder encontrar modelos según temáticas. Y cómo no, podrás encontrar el código de GPT-3 y su ya famosísimo paper “Language models are Few-Shot Learners“
2. Historias 📔
John Von Neumann y el futuro de la computación
John Von Neumann, considerado como el padre de la computación moderna, fue uno de los científicos y polímatas más relevantes del siglo XX. Durante su vida, se involucró en muy diversos ámbitos, no contento con crear la teoría de juegos, los autómatas celulares o sentar las bases de la mecánica cuántica, Von Neumann participó en el Proyecto Manhattan e inventó la arquitectura de los computadores actuales.
👦🏻 Primeros años
John von Neumann nació en Budapest en 1903 y mostró signos de genialidad desde muy joven. Se cuenta que, de niño, ya podía hablar perfectamente e incluso hacer chistes en Griego clásico y, para deleite de familiares y conocidos, era capaz de memorizar rápidamente una página de la guía telefónica y recitar a continuación todos los nombres y números de la misma.

John Von Neumann con 12 años
Tras acabar la educación secundaria en 1912, su padre intentó persuadirle para no estudiar matemáticas ya que, en su opinión, no había mucho dinero que ganar en ese ámbito. Finalmente, Von Neumann llegó a un acuerdo con su padre con el compromiso de estudiar simultáneamente Química y Matemáticas.
En su fase postdoctoral, Von Neumann tuvo la oportunidad de trabajar bajo la tutela del mismísimo David Hilbert que, como vimos en TIS #12, era el matemático más celebre en la época.
Von Neumann trabajó codo con codo con Hilbert en establecer las bases axiomáticas de las matemáticas y prueba de ellos es la publicación de 1925 “An Axiomatization of Set Theory”. Todo este trabajo quedó invalidado por los descubrimientos de Kurt Gödel con el que, casualmente, acabaría forjando una estrecha amistad. En las propias palabras de Von Neumann:
“Gödel is absolutely irreplaceable. In a class by himself.”
Pese a todo, su trabajo con Hilbert no cayó en saco roto y cristalizó en su libro The Mathematical Foundations of Quantum Mechanics (1932), en el que trataba los estados cuánticos como vectores en un Espacio de Hilbert.
🧳 Traslado a Princeton
En 1929 Von Neumann fue invitado a la Universidad de Princeton para impartir clases sobre la teoría cuántica como profesor invitado. Según sus alumnos, era un profesor terrible, propenso a escribir rápidamente en la pizarra y a borrar todo lo escrito antes de que los alumnos hubieran tenido la oportunidad de copiarlo en sus cuadernos.
Aunque no triunfara como profesor, Von Neumann se convirtió en una leyenda de Princeton por sus bromas a Einstein, su capacidad de recitar libros que había leído hace años palabra por palabra o su habilidad para calcular el resultado de programas en ensamblador de cabeza.

No sé a vosotros, pero a mí escuchar la palabra ensamblador me causa escalofríos
Tan grande llegó a ser la leyenda, que se decía que John von Neumann era probablemente la persona más inteligente que había vivido jamás.
El genial Enrico Fermi, ganador del Nobel de 1938, llegó a decir de él:
”You know, Herb, Johnny can do calculations in his head ten times as fast as I can. And I can do them ten times as fast as you can, so you can see how impressive Johnny is”
💣 El proyecto Manhattan
A finales de 1943, Von Neumann comenzó a trabajar en el proyecto Manhattan tras la invitación de Oppenheimer. Se estima que su participación en el proyecto aceleró en un año el desarrollo de la bomba atómica.
Von Neumann era un experto en física no lineal e hidrodinámica y, junto con su experiencia con explosivos, ayudó a diseñar el mecanismo de implosión de la bomba.
🎲 Teoría de Juegos
En 1944, y como ya contamos en TIS #10, John Von Neumann escribió junto con el profesor de Princeton Oskar Morgenstern, su obra magna de matemática aplicada, Theory of Games and Economic Behavior (1944). En esta publicación, continuó el trabajo que empezó por su cuenta en 1928 con su paper “Theory of Parlor Games” y que nadie hasta entonces había continuado.
El libro, con la friolera de 641 páginas, proponía la Teoría de Juegos como la Ciencia Newtoniana que subyacía a las decisiones económicas.
🤖 Computación
En los años de las postguerra, Von Neumann empezó a participar en programas industriales tan conocidos como ENIAC, una de las primeras computadoras de propósito general que, como curiosidad, pesaba 27 toneladas. Von Neumann fue el que introdujo la idea de que la computadora ejecutase programas almacenados en memoria, hito que podría considerarse como el comienzo de la historia del software.

A raíz de su trabajo en ENIAC y en otro proyectos posteriores, Von Neumann diseñó la archiconocida arquitectura de la Máquina de Von Neumann que cualquier estudiante del ámbito de la computación reconocerá:
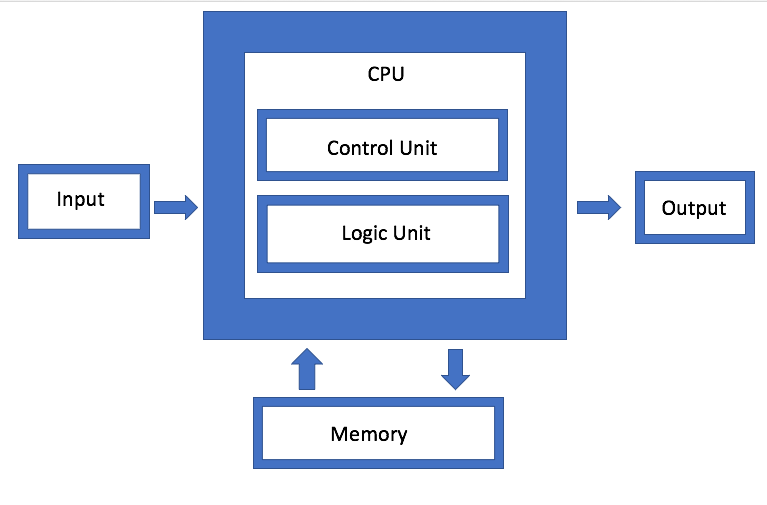
La famosa arquitectura Von Neumann
A partir de esta incursión en el mundo de la computación, Von Neumann dedicó parte de su tiempo a adentrarse en el concepto de Inteligencia Artificial.
Como ejemplo, desarrolló teorías sobre cómo usar neuronas artificiales de modo que se pudiesen hacer computaciones precisas mediante redes de componentes (una idea primigenia de red neuronal).
Él siempre dudó de si seríamos capaces de crear una Inteligencia Artificial y mostró especial interés en analizar los autómatas autorreplicables, de los que, como vimos en TIS #11, John Conway demostró su viabilidad al probar que su Juego de la Vida era una máquina Turing completa.
En uno de sus últimos escritos antes de su prematura muerte en 1957, "The Computer and the Brain" Von Neumann explicaba las dificultades que él intuía para replicar la Inteligencia humana con dispositivos electrónicos:
Computers require arithmetical precision. Brains do not. The nervous systems of living organisms have evolved to interpret and act upon vast quantities of ambiguous information without relying on computational accuracy.
En los años recientes, y debido en gran medida al tremendo impacto de los estudios de Von Neumann, se está profundizando en nuevas arquitecturas de computadores que nos permitan acercarnos a cómo realmente funciona el cerebro, tal y como a él le preocupaba y como, en cierta medida, hemos anticipado en la primera sección de la newsletter de hoy.
Paradójicamente para Von Neumann, conseguir que los ordenadores se parezcan más al cerebro, conllevará ir más a allá de la arquitectura que él mismo diseñó. A estas nuevas arquitecturas se las ha denominado Arquitecturas no-Von Neumannianas.
Inspirándose en la estructura sináptica del cerebro, investigadores de IBM han estado trabajando en una arquitectura no-Von Neumanniana para Inteligencia Artificial que permite ubicar conjuntamente la memoria y el procesamiento.
Como explica Abu Sebastian, uno de los investigadores principales del proyecto:
“If you look at human beings, we compute with 20 to 30 watts of power, whereas AI today is based on supercomputers which run on kilowatts or megawatts of power”
“In the brain, synapses are both computing and storing information. In a new architecture, going beyond von Neumann, memory has to play a more active role in computing.”
Las primeras pruebas con esta nueva arquitectura de computación están arrojando resultados prometedores y, según informan, han conseguido aumentar 200 veces el rendimiento al ejecutar un algoritmo de IA respecto a una arquitectura convencional.
Previsiblemente, y tal y como se indica en este artículo de Nature, las arquitecturas no-Von Neumannianas pueden ser el camino para alcanzar una nueva era en el mundo de la computación, pero esto requerirá el uso de nuevos materiales, nuevos dispositivos y nuevo software para dar el salto definitivo y dejar atrás la computación convencional.
Quién sabe, ¡tal vez el futuro de la computación esté aquí y no en la computación cuántica!
¡Gracias por leernos! ¡Volvemos en Septiembre!

¡Ayúdanos a difundir The Independent Sentinel compartiendo nuestras publicaciones en Redes Sociales o de cualquier otro modo que quieras!
Recuerda también que puedes dejar comentarios abajo sobre esta publicación.
¿Te has perdido alguna edición? Puedes leer todas aquí.
👉 Si quieres conocer mejor cómo funciona nuestra tecnología, no dejes de visitar nuestra serie de tutoriales publicados en Medium.
👉 Si quieres, puedes solicitar un acceso gratuito para probar nuestro producto Titan aquí https://lnkd.in/gPz-2mJ

